正規分布は統計学でよく使われる分布の一つで、さまざまな自然現象や日常のデータをモデル化するために利用されます。
ここでは、正規分布の特徴である「標準偏差」と「確率」の関係について、専門家以外の方でも理解しやすいように解説します。
正規分布とは?
正規分布は、グラフにすると左右対称の山型の形をした分布です。
具体的には、データの平均値の周りにデータが集まり、遠ざかるほどその数が減るという形を示します。
こんな感じです。
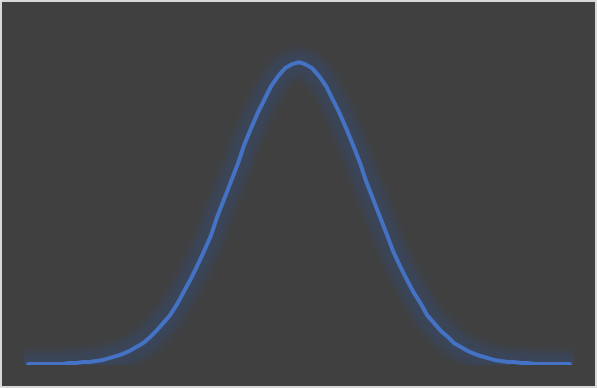
たとえば、身長やテストの点数などは正規分布に従うことが多いです。
正規分布では、平均が分布の中心を示し、そのデータの「真ん中」を表します。
一方で、「標準偏差」はデータがどれだけ広がっているか、つまりバラツキの大きさを表します。
標準偏差とは?
標準偏差は、データが平均値からどれくらい離れているかを示す指標です。
標準偏差を表す記号として、σ(シグマ)が用いられます。
正規分布では、標準偏差が分布の幅を決めます。
- 小さい標準偏差
データが平均の近くに集中している - 大きい標準偏差
データが平均から遠くまで広がっている
たとえば、テストの結果でみんなが似た点数を取っている場合、標準偏差は小さくなります。
逆に、点数に大きな差がある場合、標準偏差は大きくなります。
標準偏差の計算手順
- 各データの平均を計算
データの平均(\(μ\))は、すべてのデータの合計をデータ数で割ったものです。
$$ \mu = \frac{1}{N} \sum_{i=1}^{N} x_i $$
ここで、\(x_i\) はそれぞれのデータの値で、\(N\) はデータの数です。 - 各データと平均の差を二乗する
差を二乗することで、負の値が正に変わり、ばらつきの大きさを正の数で評価します。
$$ (x_i – \mu)^2 $$ - 二乗した差の平均を計算する(分散)
すべての差の二乗を合計し、その合計をデータ数 N で割ります。
これが分散と呼ばれるものです。
$$ 分散=\frac{1}{N}∑(x_i – \mu)^2 $$ - 分散の平方根を取る
分散の平方根を取ることで、標準偏差が求められます。
$$ σ = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i – \mu)^2} $$
ここで、\(σ\) が標準偏差です。
標本標準偏差(サンプルの場合)
データが母集団全体ではなくサンプルから得られた場合は、データ数 \(N\) の代わりに、\(N – 1\) を使って標本標準偏差を計算します。
これにより、サンプルが小さい場合でも標準偏差が過小評価されるのを防ぎます。
標本標準偏差の式は次のようになります。
$$ s = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (x_i – \bar{x})^2} $$
ここで、\(\bar{x}\) はサンプルの平均で、\(s\) は標本標準偏差です。
標準偏差と確率の関係
正規分布では、データがどこに位置するかによって、その値が発生する確率を計算することができます。
特に、平均から標準偏差の何倍離れているかによって、その範囲に含まれる確率が分かります。
- 平均 ± 1標準偏差の範囲には、全体の約68.3%のデータが含まれます。
つまり、多くのデータはこの範囲に集中しています。 - 平均 ± 2標準偏差の範囲には、約95.4%のデータが含まれます。
さらに広い範囲をカバーしますが、それでも大部分のデータです。 - 平均 ± 3標準偏差の範囲になると、全体の約99.7%が含まれます。
ほぼすべてのデータがこの範囲内に収まります。
たとえば、あるクラスのテストの平均点が70点で、標準偏差が10点だとします。
この場合、68.3%の生徒が60点から80点の間に、95.4%の生徒が50点から90点の間に点数を取っていると予測できます。
標準偏差を使って確率を考えるメリット
標準偏差を使ってデータのばらつきや確率を考えることで、何が「普通」で、何が「異常」かを判断しやすくなります。
たとえば、ある工場で製品の重量が正規分布に従うとした場合、標準偏差を使えば「平均から大きく外れた製品」を見つけ出すことができます。
これにより、品質管理の効率が上がり、不良品を発見する確率も高くなります。
実生活での応用例
正規分布と標準偏差の考え方は、さまざまな分野で応用されています。
- 教育
テストの点数分布の分析による成績評価
平均50、標準偏差10に規格化された指標が偏差値です。 - 金融
株価の変動リスクを評価
テクニカル分析で用いられる「ボリンジャーバンド」は、移動平均線と±1σ、±2σ、±3σのラインで表されます。 - 品質管理
製品の品質のバラツキの管理・不良品の発生防止
まとめ
正規分布では、データの平均と標準偏差が重要な役割を果たしています。標準偏差がデータのばらつきを表し、それによってどれだけのデータが平均から離れているか、どの程度の発生確率かが分かります。