統計学でよく登場する「p値」は、仮説検定の結果を解釈するうえで重要な指標ですが、どのように計算されるのか、初心者には少し難しいと感じるかもしれません。
p値が何を意味するのか、どのように求めるのかを具体的な例とともにまとめます。
p値とは?
p値は、帰無仮説(無効仮説)が正しいと仮定したときに、観測されたデータ(またはそれ以上に極端なデータ)が得られる確率を指します。
- 小さいp値(例: p < 0.05)
→ 観測されたデータは帰無仮説では説明がつきにくい。帰無仮説を棄却する。 - 大きいp値(例: p > 0.05)
→ 帰無仮説のもとで観測されたデータは十分に説明可能。帰無仮説を採択する。
p値の求め方
以下の手順でp値を求めることができます。
帰無仮説と対立仮説を定義
- 帰無仮説(H₀):差や効果がないと仮定する。
- 対立仮説(H₁):差や効果があると仮定する。
例: 「薬Aが薬Bよりも効果があるか」を検証する場合
H₀:薬Aと薬Bの効果は同じ
H₁:薬Aは薬Bよりも効果がある
検定統計量を計算
検定統計量は、データから仮説を検証するための値です。
t検定、z検定、カイ二乗検定など、検定方法に応じて異なる式が使われます。
例: t検定の場合
$$t = \frac{\bar{X}_1 – \bar{X}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}$$
- \(\bar{X}_1, \bar{X}_2\):2つのグループの平均値
- \(s_1^2, s_2^2\):それぞれの分散
- \(n_1, n_2\):それぞれのサンプルサイズ
棒グラフや正規分布の下での位置を確認
検定統計量からp値を求めるには、確率分布を使用します。
- t検定 → t分布
- z検定 → 標準正規分布
- カイ二乗検定 → カイ二乗分布
観測された検定統計量が分布のどの位置にあるかを計算します。
p値を計算
p値は「検定統計量が観測された値以上に極端になる確率」です。
片側検定か両側検定かによって計算が異なります。
- 片側検定:片側の尾部での確率を計算
- 両側検定:両側の尾部での確率を計算
例: t検定・両側検定の場合
$$p\text{-value} = 2 \times P(T \geq |t|)$$
片側検定と両側検定については、基本的な内容を以下の記事でまとめております。
結果を解釈
- \(p < \alpha\)(例: 0.05):帰無仮説を棄却(有意差あり)
- \(p \geq \alpha\):帰無仮説を棄却しない(有意差なし)
実際の計算例
問題
新しい薬Aが、従来の薬Bよりも有効かどうかを調べます。
薬Aと薬Bの治療効果を比較するため、次のデータを得ました。
- 薬A:平均効果値 75、標準偏差 10、サンプルサイズ 20
- 薬B:平均効果値 70、標準偏差 12、サンプルサイズ 20
解答
- 帰無仮説と対立仮説
H₀:薬Aと薬Bの効果は同じ
H₁:薬Aは薬Bよりも効果が高い - 検定統計量を計算
t検定を使用します。
$$ t = \frac{\bar{X}_A – \bar{X}_B}{\sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}}$$
$$t = \frac{75 – 70}{\sqrt{\frac{10^2}{20} + \frac{12^2}{20}}}$$
$$t \approx 1.43$$ - p値を計算
自由度(後述)を計算し、t分布表の参照により、\(p値\)を求めます。
もしくは、統計ソフトの利用により、\(p値\)を求めます。
結果として、両側検定の場合、\(p値 ≈ 0.16\)となります。 - 解釈
慣例的に \(\alpha = 0.05\) を基準とします。
\(p = 0.16 > 0.05\) のため、帰無仮説を棄却しません。
薬Aと薬Bの効果に有意な差はないと結論づけます。
自由度の計算
t検定の自由度は、等分散を仮定するか否かで計算方法が異なります。
- 等分散を仮定する場合(Studentのt検定)
自由度は以下の式により求められます。
これは両グループのサンプルサイズの合計から2を引いた値です。
$$df = n_A + n_B – 2$$ - 等分散を仮定しない場合(Welchのt検定)
Welch-Satterthwaiteの式を用いて自由度を計算し、非整数値となります。
この方法は分散が異なるグループに適しています。
$$\frac{\left( \frac{s_A^2}{n_A} + \frac{s_B^2}{n_B} \right)^2}{\frac{\left( \frac{s_A^2}{n_A} \right)^2}{n_A – 1} + \frac{\left( \frac{s_B^2}{n_B} \right)^2}{n_B – 1}}$$
t分布表を用いたp値の決定
片側検定用のt分布表(一部)は、以下のとおりです。
表の行が自由度(\(df\))、列が有意水準(\(α\))、各数値がt統計量です。
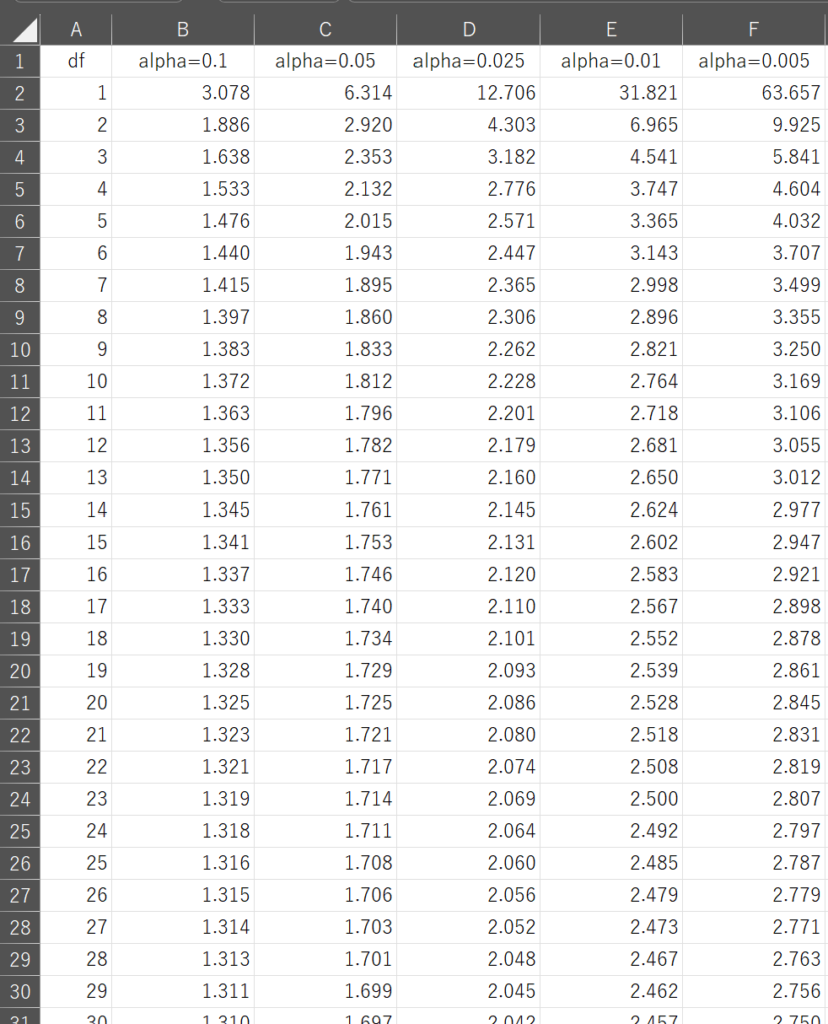
計算したt統計量が、対応する自由度と有意水準に対応するt分布表の値を超えるか確認します。
t統計量が表の値を超える場合、その\(α\)がp値の上限になります。
より小さい\(α\)を選んで正確な範囲を絞り込みます。
ExcelやPythonを使ったp値の計算
Excelの場合
T.TEST関数を使用して計算できます。
$$=\text{T.TEST}(array1, array2, tails, type)$$
引数の意味
array1、array2:t検定を行う2つのデータセットtails:片側検定か両側検定かを指定(1または2)type:t検定の種類を指定(1、2、3 のいずれか)
type引数の選択肢
type=1(対応のあるt検定)- 対応のあるデータ(ペアデータ)を比較
- 例:同じグループの前後テスト結果
type=2(等分散を仮定するt検定)- 等分散を仮定した2つの独立したグループを比較(標準的なt検定)
- 例:異なる2つのグループのデータを比較
type=3(等分散を仮定しないt検定)- Welchのt検定を実施
- 例:分散が等しいと仮定できない2つの独立グループを比較
Pythonの場合
SciPyライブラリを使用して、以下のように計算できます。
from scipy.stats import t
# 平均値、標準偏差、サンプルサイズ
mean_a, std_a, n_a = 75, 10, 20
mean_b, std_b, n_b = 70, 12, 20
# 検定統計量(t値)の計算
t_stat = (mean_a - mean_b) / ((std_a**2 / n_a + std_b**2 / n_b) ** 0.5)
# Welch-Satterthwaiteの自由度
df = ((std_a**2 / n_a + std_b**2 / n_b) ** 2) / (
((std_a**2 / n_a) ** 2) / (n_a - 1) + ((std_b**2 / n_b) ** 2) / (n_b - 1)
)
# p値の計算(両側検定)
p_value = 2 * t.sf(abs(t_stat), df)
print(f"t値: {t_stat:.3f}, p値: {p_value:.3f}")以下のとおり、データのリストから算出することもできます。
import numpy as np
from scipy.stats import ttest_ind
# ランダムデータを生成
np.random.seed()
data_a = np.random.normal(loc=75, scale=10, size=20) # 平均75、標準偏差10の確率分布に従うデータ
data_b = np.random.normal(loc=70, scale=12, size=20) # 平均70、標準偏差12の確率分布に従うデータ
# t検定
t_stat, p_value = ttest_ind(data_a, data_b)
print(f"t値: {t_stat:.3f}, p値: {p_value:.3f}")
上記コードでは、毎回異なるデータをランダムに生成するため、コードを実行する度に結果が変わります。
おわりに
p値は統計学的仮説検定で重要な指標ですが、手計算では難しい場合もあります。t分布やz分布に基づく計算を理解し、ExcelやPythonのツールを活用すると効率的です。





