書籍 人間関係の悩みから解放！
直感に反する確率
便利！SQLのWITH句
【Excel】FILTER関数便利すぎ！
スポンサーリンク

ロジスティック回帰とは？分かりやすくまとめ【Pythonサンプルコード付き】

2025.02.15
記事内に広告が含まれています。

ロジスティック回帰（Logistic Regression）は、分類問題を解くための機械学習アルゴリズムです。

名前に「回帰」と付いていますが、実際には回帰ではなく分類に使われます。

Contents
  1. ロジスティック回帰の概要
  2. ロジスティック回帰の数学的な仕組み
  3. ロジスティック回帰をPythonで実装
  4. ロジスティック回帰の解釈
  5. ロジスティック回帰の応用
  6. 確率モデルの導出
  7. まとめ
スポンサーリンク

ロジスティック回帰の概要

ロジスティック回帰は、確率モデルを用いて「あるデータが特定のカテゴリに属する確率」を求めます。

例えば以下のような問題に適用可能です。

  • メールがスパムかどうか（0 = 非スパム, 1 = スパム）
  • 顧客が商品を購入するか（0 = 購入しない, 1 = 購入する）
  • 患者が病気かどうか（0 = 健康, 1 = 病気）

このように、2値分類（二項分類）が主な用途です。

スポンサーリンク

ロジスティック回帰の数学的な仕組み

ロジスティック回帰では、以下のような式で確率 \(p\) を求めます

$$p = \frac{1}{1 + e^{-(w_0 + w_1x_1 + w_2x_2 + … + w_nx_n)}}$$

この関数をシグモイド関数（sigmoid function）といいます。

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$​

シグモイド関数の特徴は、以下のとおりです。

  • 値を 0 から 1 の範囲に変換する
  • \(z\) が大きいと \(\sigma(z)\) は 1 に近づく
  • \(z\) が小さいと \(\sigma(z)\) は 0 に近づく

分類のルールは、以下のとおりとなります。

  • \(p\) が 0.5 以上なら「1」
  • \(p\) が 0.5 未満なら「0」

ロジスティック回帰をPythonで実装

必要なライブラリをインストール・インポート

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

サンプルデータの準備

ここでは「顧客の年齢と収入をもとに、商品を購入するかどうかを予測する」というデータを作成します。

# サンプルデータの作成
np.random.seed(42)
num_samples = 200

# 年齢（18歳〜65歳）
age = np.random.randint(18, 65, num_samples)

# 収入（200万〜1000万）
income = np.random.randint(200, 1000, num_samples)

# 購入（1: 購入する, 0: 購入しない） → 収入と年齢が高いと購入確率が高くなる
purchase = (income > 600) & (age > 30)
purchase = purchase.astype(int)

# データフレーム化
df = pd.DataFrame({'Age': age, 'Income': income, 'Purchase': purchase})

# データの確認
print(df.head())

コードの実行結果は以下のとおりです。

   Age  Income  Purchase
0   56     709         1
1   46     585         0
2   32     586         0
3   60     312         0
4   25     812         0

データの可視化

データを可視化してみます。

plt.figure(figsize=(8,6))
plt.scatter(df['Age'], df['Income'], c=df['Purchase'], cmap='bwr', alpha=0.7)
plt.xlabel("Age")
plt.ylabel("Income")
plt.title("Age vs Income (Purchase Decision)")
plt.colorbar(label="Purchase (0=No, 1=Yes)")
plt.show()

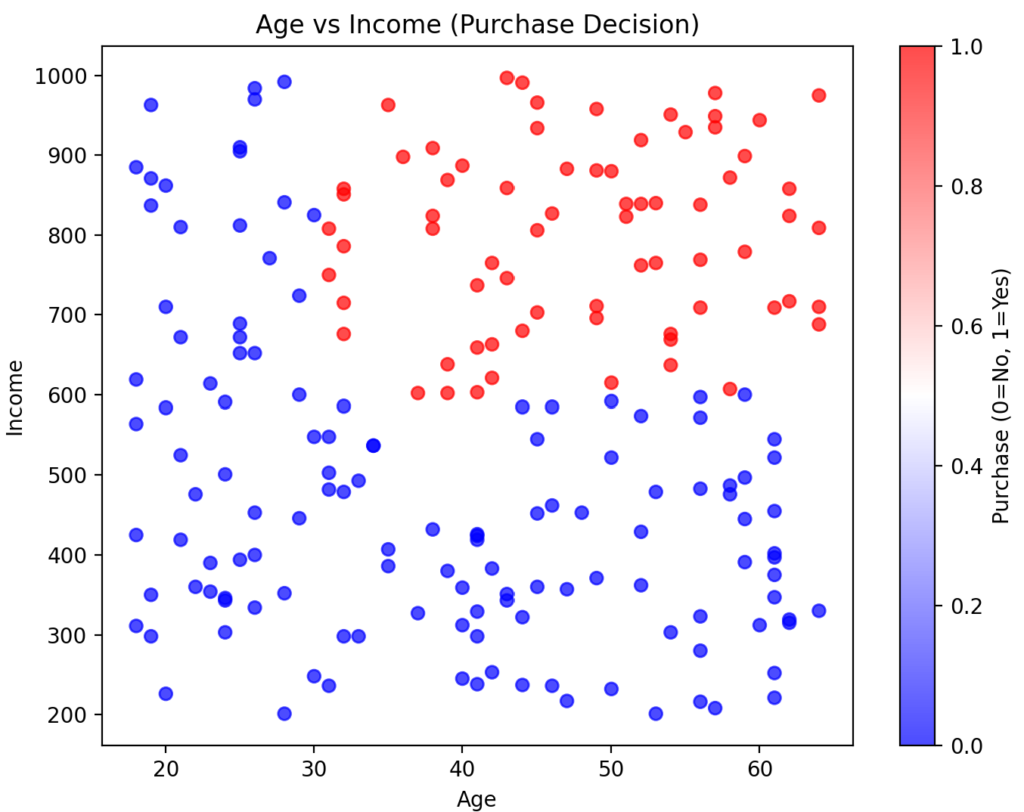
実行結果の画像は、以下のとおりです。

Yes（購入）は赤、No（非購入）は青のプロットです。

ロジスティック回帰モデルの作成と学習

サンプルデータでモデルの学習を行います。

# 特徴量とターゲット変数を設定
X = df[['Age', 'Income']]
y = df['Purchase']

# 訓練データとテストデータに分割（80% 訓練, 20% テスト）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの作成
model = LogisticRegression()

# モデルの学習
model.fit(X_train, y_train)

モデルの評価

モデルの評価を行います。

# 予測
y_pred = model.predict(X_test)

# 正解率（Accuracy）
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")

# 混同行列
conf_matrix = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(conf_matrix)

正解率と混同行列の出力結果は以下のとおりです。

Accuracy: 0.88
Confusion Matrix:
[[24  4]
 [ 1 11]]

ロジスティック回帰の解釈

ロジスティック回帰モデルは、特徴量ごとの影響度（重み係数）を確認できます。

# 係数と切片
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

Coefficients: [[0.16839543 0.01591152]]
Intercept: [-18.06854142]
  • 係数が正の場合 → その特徴量が大きくなると「1」（購入する）の確率が上がる
  • 係数が負の場合 → その特徴量が大きくなると「0」（購入しない）の確率が上がる

例えば、Age や Income の係数が大きい場合、年齢や収入が増えると商品購入の確率が高まることが分かります。

ロジスティック回帰の応用

ロジスティック回帰は、以下のような多くの場面で使われます。

マーケティング分析
  • 顧客が商品を購入する確率の予測
  • 広告クリック率の予測
医療データ分析
  • 患者が病気にかかるかどうかの予測
  • ある治療が成功する確率の推定
金融データ分析
  • ローン申請の審査（返済能力の予測）
  • クレジットカードの不正利用検出

確率モデルの導出

ここからは、ロジスティック回帰の確率モデル（数式）の導出について、少し詳しくまとめます。

前述のとおり、ロジスティック回帰では、確率 \(P(Y=1|X)\) を求めるために、シグモイド関数を使います。

$$P(Y=1|X) = \frac{1}{1 + e^{-(w_0 + w_1 X_1 + w_2 X_2 + … + w_n X_n)}}$$

この式がどのようにして導かれるのか、ベイズの定理を使って説明します。

ベイズの定理とは？

ベイズの定理は、条件付き確率を求める公式です。

$$P(Y|X) = \frac{P(X|Y) P(Y)}{P(X)}$$

これを使って、ロジスティック回帰の確率モデルを導きます。

確率の設定

ロジスティック回帰では、2つのクラス（たとえば \(Y=1\) と \(Y=0\)）にデータを分類したいので、それぞれの確率を考えます。

  • 事前確率（クラスの発生確率）
    • \(P(Y=1) = p\)（クラス1の割合）
    • \(P(Y=0) = 1 – p\)（クラス0の割合）
  • 尤度（likelihood）（Xの発生確率）
    • \(P(X|Y=1)\)（クラス1のときの X の分布）
    • \(P(X|Y=0)\)（クラス0のときの X の分布）

ロジスティック回帰では、\(X\) がクラスごとに正規分布しているとは仮定せず、指数関数型のモデル（一般化線形モデル）を考えます。

事後確率の計算

ベイズの定理を使って、データ \(X\) が与えられたときの \(Y=1\) の確率を求めます。

$$P(Y=1 | X) = \frac{P(X | Y=1) P(Y=1)}{P(X)}$$​

同様に、\(Y=0\) の確率も求められます。

$$P(Y=0 | X) = \frac{P(X | Y=0) P(Y=0)}{P(X)}$$​

この2つの確率の比（オッズ）を求めます。

$$\frac{P(Y=1 | X)}{P(Y=0 | X)} = \frac{P(X | Y=1) P(Y=1)}{P(X | Y=0) P(Y=0)}$$​

ここで、対数を取ると 次の形になります。

$$\log \left( \frac{P(Y=1 | X)}{P(Y=0 | X)} \right) = \log P(X | Y=1) – \log P(X | Y=0) + \log P(Y=1) – \log P(Y=0)$$

尤度の仮定

ロジスティック回帰では、指数型分布族（exponential family） の尤度を仮定します。

具体的には、条件付き確率 \(P(X | Y)\) を指数関数の形で表します。

$$P(X | Y = y) = h(X) \exp \left( \eta_y^T X – A(\eta_y) \right)$$

ここで

  • \(h(X)\) ：基底分布
  • \(X\) ：特徴量ベクトル（説明変数）
  • \(\eta_y\) ：自然パラメータ
  • \(A(\eta_y)\) ：正規化項

特に、線形関数 の形を仮定すると

$$\log P(X | Y=1) – \log P(X | Y=0)$$

$$=(\log h(X)+\eta_1^T X−A(\eta_1​))−(\log h(X)+\eta_0^T X−A(\eta_0​))$$

$$= \eta_1^T X – \eta_0^T X +C$$

つまり、線形結合の形になります。

事前確率の対数の差

事前確率 \(P(Y)\) は、単なる定数なので、

$$\log P(Y=1) – \log P(Y=0)$$

は スカラー値の定数 です。

線形モデルの形

したがって、全体の式は次のように整理できます。

$$\log \left( \frac{P(Y=1 | X)}{P(Y=0 | X)} \right) = (\eta_1 – \eta_0)^T X + C + \log P(Y=1) – \log P(Y=0)$$

ここで、係数を次のように置き換えます。

  • \(w_0 = C + \log P(Y=1) – \log P(Y=0)\)（バイアス項）
  • \(w = \eta_1 – \eta_0\)​（重みベクトル）

結果として、ロジット変換（logit transformation）の形になります。

$$\log \left( \frac{P(Y=1 | X)}{P(Y=0 | X)} \right) = w_0 + w_1 X_1 + w_2 X_2 + … + w_n X_n$$​

これは ロジスティック回帰の線形モデル です。

\(P(Y=1 | X)\) を \(p\) 、\(P(Y=0 | X)\) を \(1 – p\) と置き換えることで、以下の式が導かれます。

$$p = \frac{1}{1 + e^{-(w_0 + w_1x_1 + w_2x_2 + … + w_nx_n)}}$$

まとめ

  • ロジスティック回帰は分類（特に二値分類）に使われる
  • シグモイド関数を用いて、確率を計算し「0 or 1」を判定する
  • Pythonのscikit-learn を使えば簡単に実装できる
  • マーケティング・医療・金融など様々な分野で応用できる
タイトルとURLをコピーしました