統計学や機械学習でよく登場する「ベルヌーイ分布(Bernoulli Distribution)」についてまとめます。
ベルヌーイ分布とは?
ベルヌーイ分布とは、試行の結果が2つに分かれる確率分布です。
例えば、以下のような試行の結果です。
- コインを投げて「表」か「裏」が出る
- サイコロを振って「6が出た」か「6が出なかった」
- 商品が「購入された」か「購入されなかった」
- 受験に「合格した」か「不合格だった」
このように、成功(1)または失敗(0)のどちらかしか起こらない試行において、その確率をモデル化したものがベルヌーイ分布です。
ベルヌーイ分布の確率関数
ベルヌーイ分布の確率質量関数(PMF)は次のように表されます。
$$P(X = x) = p^x (1 – p)^{1 – x}, \quad x \in \{0,1\}, \quad 0 \leq p \leq 1$$
ここで
- \(X\) は確率変数(成功 or 失敗)
- \(p\) は成功の確率(例:コインで表が出る確率)
- \(x = 1\) のとき \(P(X = 1) = p\)(成功の確率)
- \(x = 0\) のとき \(P(X = 0) = 1 – p\)(失敗の確率)
具体例
例えば、コインを投げたときに「表(成功)」が出る確率が 0.6 だとすると、以下のとおりとなります。
- \(P(X=1) = 0.6\)(表が出る確率)
- \(P(X=0) = 1 – 0.6 = 0.4\)(裏が出る確率)
ベルヌーイ分布の期待値と分散
確率分布を扱う際、重要な指標として期待値(平均値)と分散があります。
- 期待値(平均値):\(E[X] = p\)
- 分散:\(Var(X) = p(1 – p)\)
期待値の解釈
ベルヌーイ分布の期待値 \(E[X]\) は、長期間試行したときに平均的に得られる「1の割合」となります。
例えば、コインの表が出る確率が \(0.6\) の場合、\(100\)回試行すると、おおよそ\(60\)回が表(\(1\))になると期待できます。
分散の解釈
分散 \(p(1 – p)\) は、データの散らばり具合を示します。
- \(p = 0.5\) のとき、分散は最大(\(0.25\))になり、試行結果はバラつきやすい。
- \(p = 0\) または \(p = 1\) のとき、分散は \(0\) になり、結果は確定的(常に\(0\)または\(1\))になる。
ベルヌーイ分布の活用例
ベルヌーイ分布はシンプルながら、様々な分野で使われます。
機械学習・AI
- 分類問題:「スパムメールかどうか」のような2値分類の確率モデル
- ロジスティック回帰:出力が0または1の確率で決まる回帰モデル
マーケティング・A/Bテスト
- 購入確率のモデル化:ユーザーが「購入する(1)」か「しない(0)」
- 広告クリック率:広告がクリックされる(1)or されない(0)
医学統計・疫学
- 新薬の有効性検証:「効果がある(1)」or「効果がない(0)」
- 病気の発生率モデル:「発症(1)」or「非発症(0)」
Pythonでベルヌーイ分布をシミュレーション
Pythonを使って、ベルヌーイ分布の乱数を発生させてみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
# 成功確率 p = 0.6 のベルヌーイ分布
p = 0.6
sample_size = 1000 # 1000回試行
samples = bernoulli.rvs(p, size=sample_size)
# 結果の可視化
plt.hist(samples, bins=[-0.5, 0.5, 1.5], edgecolor='black', density=True, rwidth=0.8)
plt.xticks([0, 1], ['Failure (0)', 'Success (1)'])
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.title(f'Bernoulli Distribution (p={p})')
plt.show()
このコードでは以下の処理を行います。
bernoulli.rvs(p, size=1000)で 1000 回の試行をシミュレーションplt.hist()で結果をヒストグラム表示
成功確率 \(p = 0.6\) なので、計算上、\(1\)の割合が \(60%\)、\(0\)の割合が \(40%\) になるはずです。
コードの実行結果のヒストグラムは以下の画像のとおりです。
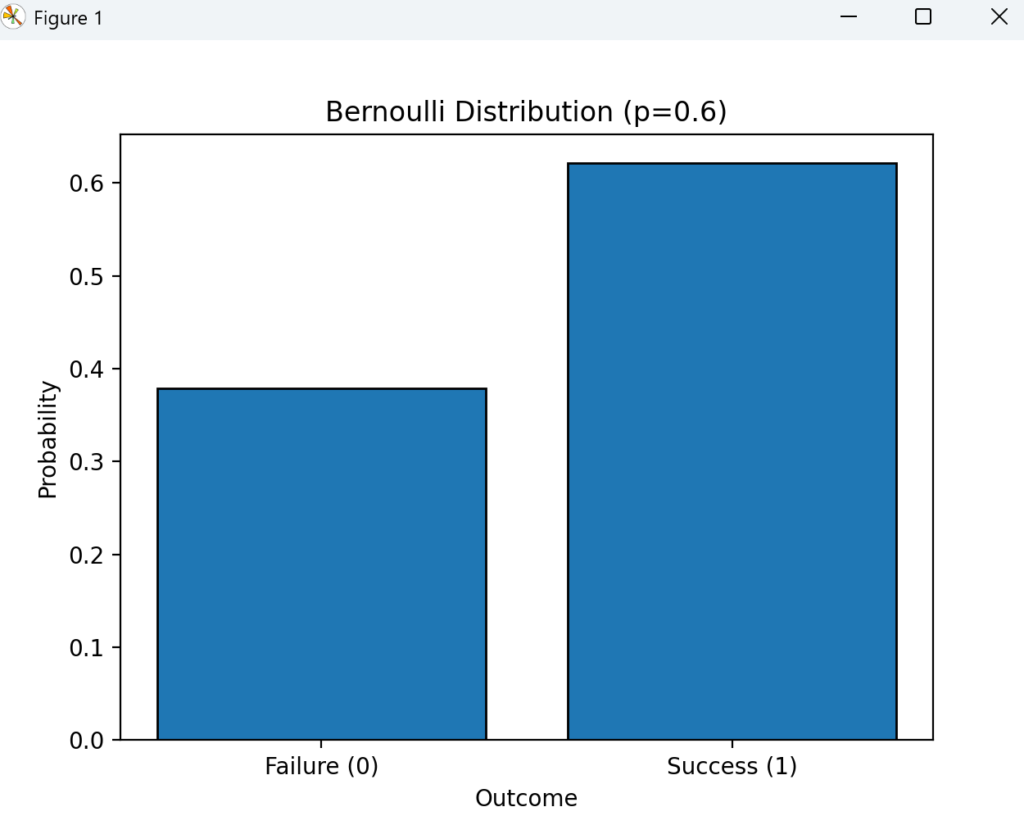
まとめ
- ベルヌーイ分布は、結果が「成功(1)」または「失敗(0)」の確率分布。
- 確率質量関数は \(P(X=x) = p^x(1-p)^{1-x}\)
- 期待値は \(E[X] = p\)、分散は \(Var(X) = p(1 – p)\)。
- A/Bテスト、機械学習、疫学など様々な分野で活用される。
- Pythonで簡単にシミュレーションできる。
ベルヌーイ分布は基礎的な確率分布ですが、機械学習の分類問題やA/Bテストなど、多くの応用があります。




