【Python】重回帰分析を行うコード

重回帰分析は、複数の説明変数を使用して目的変数を予測する手法で、ビジネスや研究で広く利用されています。

本記事では、Pythonを使った重回帰分析の基本的な手順をまとめ、データ準備からモデル構築、評価までのプロセスを具体的なコード例とともに紹介します。

Contents

ライブラリ
データの準備
説明変数と目的変数の分割
データの分割
モデルの構築と学習
モデルの評価
可視化
実行結果
まとめ

ライブラリ

Pythonで重回帰分析を行うには、以下のライブラリを使用します。

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

データの準備

まず、分析対象となるデータを用意します。

以下の例では架空のデータを作成します。

# サンプルデータの作成
data = {
    'Feature1': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
    'Feature2': [2, 4, 6, 8, 10, 11.5, 12, 14, 17, 21],
    'Feature3': [1, 3, 5, 7, 9, 11.5, 12, 14, 18, 22],
    'Target': [2.2, 4.5, 6.3, 8.0, 10.1, 12.2, 14.5, 15.8, 17.8, 20.5]
}

# DataFrameに変換
df = pd.DataFrame(data)

# データ確認
print(df)

   Feature1  Feature2  Feature3  Target
0         1       2.0       1.0     2.2
1         2       4.0       3.0     4.5
2         3       6.0       5.0     6.3
3         4       8.0       7.0     8.0
4         5      10.0       9.0    10.1
5         6      11.5      11.5    12.2
6         7      12.0      12.0    14.5
7         8      14.0      14.0    15.8
8         9      17.0      18.0    17.8
9        10      21.0      22.0    20.5

説明変数と目的変数の分割

説明変数（特徴量）と目的変数（ターゲット）を分けます。

# 説明変数と目的変数の分割
X = df[['Feature1', 'Feature2', 'Feature3']]  # 説明変数
y = df['Target']  # 目的変数

データの分割

データをトレーニングデータとテストデータに分割します。

# データ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 分割後のデータサイズ確認
print("Training data size:", X_train.shape)
print("Test data size:", X_test.shape)

Training data size: (8, 3)
Test data size: (2, 3)

モデルの構築と学習

LinearRegression を使って重回帰モデルを構築し、トレーニングデータで学習させます。

# モデル構築
model = LinearRegression()

# モデル学習
model.fit(X_train, y_train)

# 学習済みモデルの係数と切片
print("Coefficients:", model.coef_)
print("Intercept:", model.intercept_)

Coefficients: [ 1.83944705 -0.31233177  0.36001043]
Intercept: 0.7144392279603498

モデルの評価

テストデータを使ってモデルの性能を評価します。

# 予測
y_pred = model.predict(X_test)

# 評価指標
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("Mean Squared Error:", mse)
print("R-squared:", r2)

Mean Squared Error: 0.2428843116622033
R-squared: 0.9945076756930928

可視化

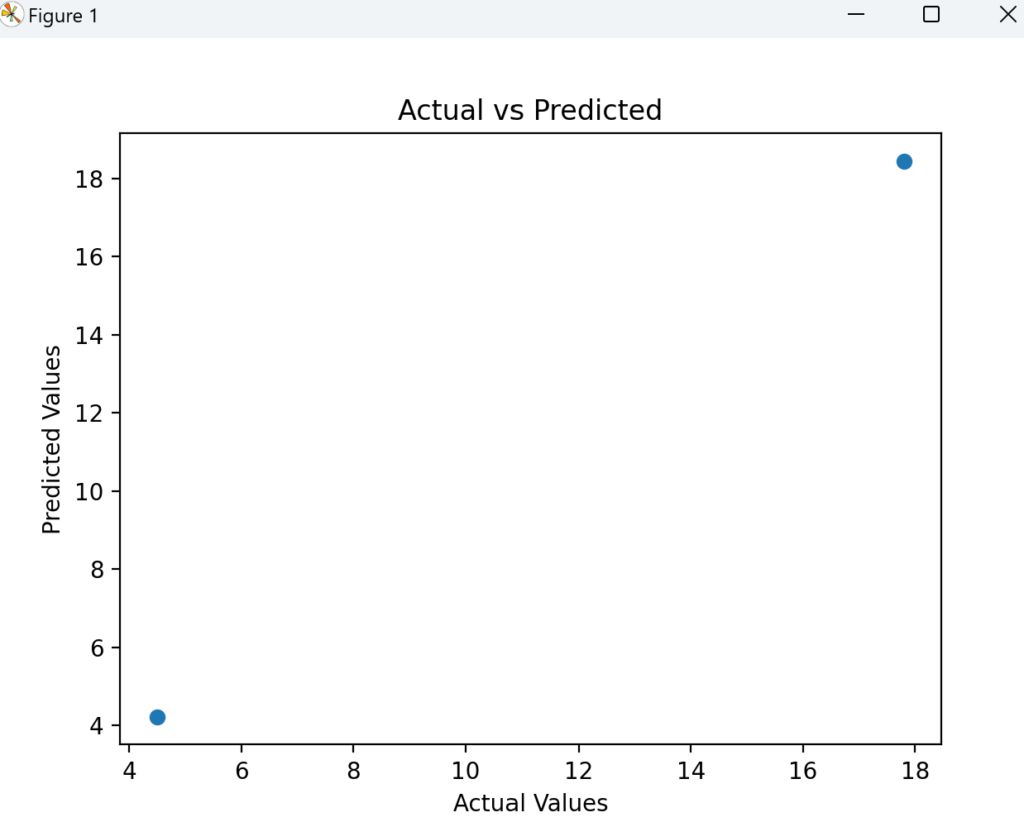
予測結果を可視化することで、モデルの精度を直感的に理解できます。

import matplotlib.pyplot as plt

# 実測値 vs 予測値のプロット
plt.scatter(y_test, y_pred)
plt.xlabel("Actual Values")
plt.ylabel("Predicted Values")
plt.title("Actual vs Predicted")
plt.show()