べき分布(power-law distribution)は、データの分布が特定のスケールに従う場合に使われる統計学の概念です。
主に自然現象や社会現象などで見られるもので、少数の大きな値と多数の小さな値が特定のパターンに従う分布を指します。
ここでは、べき分布について詳しく説明します。
べき分布の定義
べき分布は、確率密度関数 \(P(x)\) が次の形で表される分布です。
$$P(x) = C \cdot x^{-\alpha}$$
ここで、
- \(x\) は変数で、通常は正の値を取ります。
- \(\alpha\) はべき指数と呼ばれる定数で、分布の傾きを決定します。
- \(C\) は正規化定数で、確率密度関数が全体として1になるように調整されます。
べき分布の特徴
べき分布にはいくつかの特徴があります。
- スケール不変性
べき分布はスケール変換に対して不変です。
つまり、変数をスケールアップまたはスケールダウンしても、分布の形は変わりません。 - 長い尾
べき分布は右に長い尾を持ちます。
他の確率分布と比較して、大きな値が出現する確率が無視できない高さです。 - フラクタル構造
べき分布を持つデータは、自己相似的なフラクタル構造を示すことがよくあります。
グラフにすると以下のようになります。
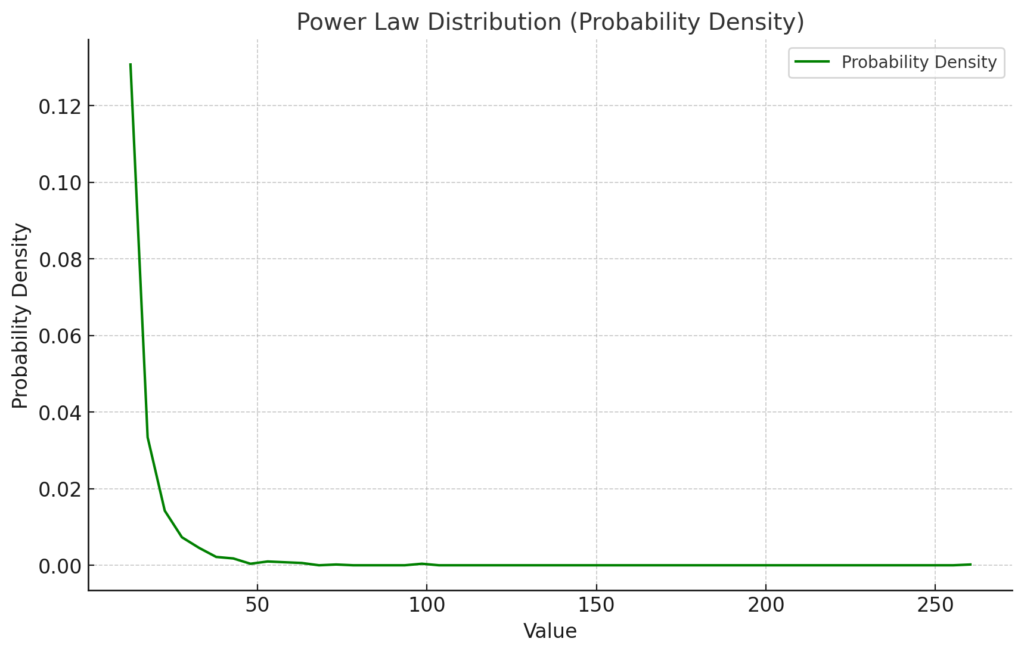
べき分布の応用例
べき分布は多くの分野で見られ、その中でも特に注目すべき応用例を以下に挙げます。
- 自然現象
地震のマグニチュード、山の高さ、洪水の規模などがべき分布に従うことが知られています。 - 社会現象
都市の人口分布、企業の売上高、個人の所得分布などもべき分布に従います。 - インターネット
ウェブページのリンク数、ソーシャルネットワークの接続数などもべき分布を示すことがあります。
べき分布のモデリングと解析
べき分布をデータに適用する際には、以下のステップを踏むことが一般的です。
- データの収集
対象となるデータを集めます。 - 対数-対数プロット
データの分布を視覚的に確認するために、対数-対数プロットを作成します。
このプロットで直線に近い場合、べき分布が適していることが示唆されます。 - べき指数の推定
べき指数 \(\alpha\) を推定します。
これは通常、最尤推定法や最小二乗法を用いて行います。 - 適合度の評価
べき分布がデータにどの程度適しているかを評価します。
適合度を評価するためには、コルモゴロフ・スミルノフ検定やジ・テストなどの統計的手法を用います。
まとめ
べき分布は、自然界や社会現象の多くの側面を理解する上で非常に重要なツールです。スケール不変性や長い尾の特性を持つため、大きな値の出現を予測するのに適しています。べき分布を正しく理解し、適用することで、データ解析やモデリングにおいて有益な洞察を得ることができます。





